Calculating Tool Engagement Angle, Radial Depth of Cut
August 18, 2012, 11:14 amArticle Summary
Eldar Gerfanov (Admin)
August 18, 2012, 11:14 am
August 20, 2012, 11:52 am
40242
Public
Author Summary
Sat April 26, 2025, 12:19 am
Sat April 26, 2025, 12:19 am
Here i will show you how to calculate Tool Engagement Angle using tool diameter and Width Of Cut (radial deopth of cut)
Lets first draw a pretty image that shows us everything we need.
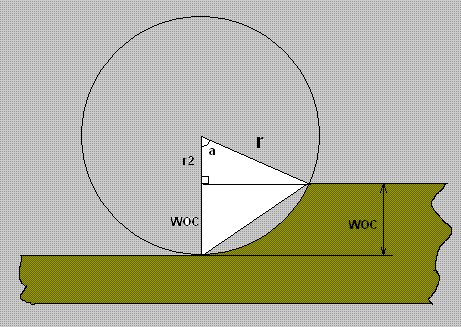
Where:
- r: Radius of the cutter = Diamater /2
- a: TEA - Enagagement angle we are trying to find here
- WOC: Width of cut or RADIAL Depth of Cut
- r2: The difference between r and WOC, r=r2+WOC
Below we develop 2 formulas that allow us to find TEA and WOC
Task 1: Find WOC (Radial Depth of Cut) knowing tool engagement angle and diameter of the tool
Solution:
WOC=r-r2
r2=COS(a) * r
COS(a)=r2 / r
r2=COS(a) * R
| Diamater | Diameter | |||
| WOC = |
|
- |
COS(a) * |
|
| 2 | 2 |
or if we move Diameter/2 outside of brackets:
| Diamater |
| |
| | ||||
| WOC = |
|
* |
| |
1- |
COS(a) | | |
| 2 |
| |
| |
or if we replace Diameter/2 with radius:
WOC=r * (1-COS(a))
Task 2: Find engagement angle knowing WOC (Radial Depth of Cut) and diameter of the tool
Solution:
WOC = r - r2
r2 = COS(a) * r
COS(a)= r2 / r
a = COS-1( r2 / r )
a = COS-1( ( r - WOC) / r )
a = COS-1( 1 - WOC / r )
or
a = COS-1( 1 - WOC / Dia/2 )
Thats it folks
You shall be surprised but those two formulas work also for TEA bigger than 90 Degree
Divyang
Nice, Thanks. Could you please show how to  calculate cutter engagement angle when a tool is performing pocket machining using a curvilinear or spiral like tool path.
Eldar Gerfanov (Admin)
Updated by: Eldar Gerfanov (Admin)April 10, 2015, 11:43 pm
Divyang
Hi, Thank you very much Eldar Gerfanov for the reply. But still it is very difficult for me to comprehend what you exactly want to say. My question is very simple. Say, I want to machine a circular pocket (with diameter, D) and tool (diameter, d) with spiral toolpath toolpath (R,theta), where R is the radius for corresponding theta. For one convolution theta varies from 0 to 230 degrees. and step over is kept as say 'S'.  How to calculate the cutter engagement angle in this case. I have tried but things are getting complicated for me as for each pass the surface generated by the preceding convolution has to be taken into account. If possible, a rough sketch would be helpful. once again thanks.
Eldar Gerfanov (Admin)
Updated by: Eldar Gerfanov (Admin)May 3, 2015, 2:06 pm
Jim
I'm sure this is not where I'm supposed to post, but I hope somone can help me. I'm having problems opening/installing HSM Advisor in 64 bit vista. Comapatibility mode is un usefull. Any help is much appreciated.
Eldar Gerfanov (Admin)
Hank
Is there an app to calculate Tool Engagement Angle?